图解基础数学知识-gif几何动图趣解——秒懂几何原理

在看学大教育知乎专栏是，发现一些好的数学gif动图。原来数学原理阐释的可以如此简单。之前读书的时候，数学公式基本是靠死记硬背和刷题的。早两年，看学渣课堂(好像是叫这个名字），里面讲的数学课，就很好理解

基础几何

1582年，明神宗万历十年，有一个叫利玛窦的意大利人来到中国。之后徐光启意识到了《几何原本》代表的这种西方科学范式的方法论非常的重要。几何学代表的这种严密的逻辑推理方法是科学研究的基础。，他学习《几何原本》之后，利用这几何知识就精准的预测了1610年的日食，搞得朝野振动，一时间西方科学名声大振，然后一大波西方科学著作潮水般的被翻译进来了。但是到了康熙七年，大统历与时宪历(西洋新历)之间进行了一场终极大PK。在众多官员的见证下，时宪历成功预测了一起日全食。

果大地如圆球，则四旁与在下国土洼处之海水，不知何故得以不倾？真如西人所言，则西洋皆为鱼鳖，而若望不得为人矣。

想想我小时，学数学，基本就是考背公式，然后做试卷，到高中，还有 题库、宝典什么的刷题。现在感觉书是白读了。

勾股定理证明

勾股定理指的是直角三角行直角边的平方和等于斜边的平方，即：A²+B²=C²。

勾股定理现约有500种证明方法，毕达哥拉斯是第一个对此定理进行了严格证明的人。

看完下面2幅图，你对这个定理有没有更加深刻的认识？

圆的面积计算

阿基米德（公元前287年—公元前212年），世界三大数学家(阿基米德和高斯、牛顿）。他利用“逼近法”算出球面积、球体积、抛物线、椭圆面积，后世的数学家依据这样的“逼近法”加以发展成近代的“微积分”。

那为什么圆的面积公式是πr²？

是这样的，把圆解剖为一个三角形。底边是周长，然后根据三角形的面积推出圆的面积。

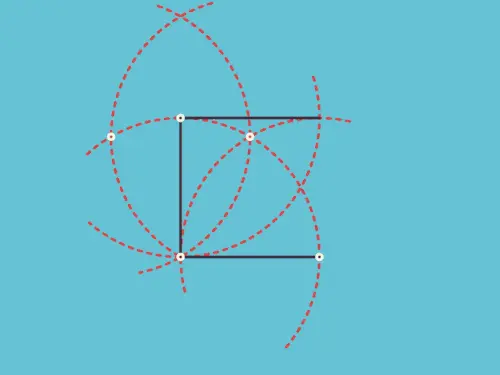
如何画圆为方

图形变换

任意四边形剪成一个长方形

将两个大小不一的正方形拼剪成一个大正方形：

将一个正三角形拼剪成正方形：

多边形内角和

三角形的内角和为啥等于180°？而外角和等于360°？

任意多边形的外角和都等于360°

解析几何

几何-圆锥曲线

阿波罗尼奥斯（Apollonius of Perga，约公元前262～190年），古希腊数学三大神(阿波罗尼、欧几里得、阿基米德)之一。

著作《圆锥曲线论》是古代世界光辉的科学成果，它将圆锥曲线的性质网罗殆尽(使用纯几何方法已经取得了今天高中数学中关于圆锥曲线的全部性质和结果)。

古希腊数学家阿波罗尼斯采用平面切割圆锥的方法来研究这几种曲线。

• 亏曲线：用垂直于锥轴的平面去截圆锥，得到的是圆；把平面渐渐倾斜，得到椭圆；

• 齐曲线：当平面倾斜到“和且仅和”圆锥的一条母线平行时，得到抛物线；

• 超曲线：用平行于圆锥的轴的平面截取，可得到双曲线的一支（把圆锥面换成相应的二次锥面时,则可得到双曲线）。

代数-圆锥曲线

在笛卡尔平面上，二元二次方程 Ax²+Bxy+Cy²+Dx+Ey+F=0的图像称为二次曲线。

根据判别式的不同，包含了椭圆、双曲线、抛物线以及各种退化情形。

焦点+准线-圆锥曲线

给定一点P，一直线L以及一非负实常数e，则到P的距离与L距离之比为e的点的轨迹是圆锥曲线。

根据e的范围不同，曲线也各不相同。具体如下：

• e=0，轨迹为一点或一个圆；

• e=1（即到P与到L距离相同），轨迹为抛物线；

• 0<e<1，轨迹为椭圆；

• e>1，轨迹为双曲线。

如果逐步介绍，可能要晕菜，下的GIF图，应该非常好理解

双曲线

将双曲线表现成3D形式，也许你不相信，它完全是用直线画成的，可以做出这样的效果：

再来个现实版本的

胖子应该过了这个门，比如这么胖的

三角函数

在Y轴上画正弦（红），在x轴上画余弦（蓝），那么在XY轴平面上的环形就是这样的

sin和cos的知识点你还记得吗？同前一原理，但更简单。看着是不是开始有点晕了？

这是将sin和cos运用到三角。看着估计更晕了。

余弦是正弦的衍生物

正切线

笛卡尔坐标，它表示了点在空间中的位置，但却和直角坐标有区别，两种坐标可以相互转换。 在数学里，笛卡尔坐标系，也称直角坐标系，是一种正交坐标系。 在原本的二维直角坐标系，再添加一个垂直于 x-轴，y-轴的坐标轴，称为 z-轴。就构成了三维笛卡尔坐标系。

将一个公式从笛卡尔坐标转换成轴坐标：

参考文章：

数学原来有套路！这10张动图，让孩子瞬间爱上数学！ https://zhuanlan.zhihu.com/p/29565201

转载本站文章《图解基础数学知识-gif几何动图趣解——秒懂几何原理》,
请注明出处：https://www.zhoulujun.cn/html/theory/Mathematics/Geometry/7458.html